[無料ダウンロード! √] 2次関数 平行移動 280538-2次関数 平行移動 応用
2次関数とは? 関数は「グラフが命!」 定義域・値域とは? 関数f(x)とは? y=ax^2のグラフ(下に凸、上に凸) y=ax^2qのグラフ1; 例題 上で説明した内容を使って、問題を解いてみましょう。 標準放物線の平行移動(頂点に着目) で出てきた問題を解いてみます。 例題 放物線 y = 3x2 − 12x 10 y = 3 x 2 − 12 x 10 を x 軸方向に 1 1 、 y 軸方向に −2 − 2 だけ平行移動した放物線の2次関数の平行移動を使った問題 y=ax²のグラフを 平行移動 して、 ・ "y=a (xp)²" ・ "y=ax²+q" ・ "y=a (xp)²q" の形にすることはすでに学習済みかと思います。 ここでは、これらの平行移動のテクニックを使った練習問題を一緒に解いて、理解を深めて

X 2 Y 1 Descubre Como Resolverlo En Qanda
2次関数 平行移動 応用
2次関数 平行移動 応用-関数\(y=x\sin x\)を\(x\)軸方向に3、\(y\)軸方向に1平行移動したグラフの方程式を求めよ。 二次関数\(y=\left(x2\right)^24\)の頂点の座標を求めよ。 答えは一番最後にあるよ!2 2 次関数という新しい関数を学習する前段階として、 「関数」の新しい表記を導入します。 一般に、 y y が x x の関数であることを f f などの記号を使って、 y = f (x) y = f ( x) と表します。 また、関数 f (x) f ( x) において、 x x に a a を代入した値を f (a) f ( a) で表します。 例 f (x) = x2 − 2x 5 f ( x) = x 2 − 2 x 5 において、 f (−3) f ( − 3) の値は、 f (−3) = (−3)2 − 2×



放物線ヨコ平行移動が式と逆な感じがする話題をサマータイムと絡めて話してみた すうがくブログ 式変形ch
2次関数y=ax 2 bxcのグラフは、aが0より大きい場合(a>0)は下に凸、aが0より小さい場合(a 0)は上に凸の形になります。下図をみてください。2次関数のグラフを示しました。 2次関数の平行移動 原点を頂点とする2次関数y=ax 2 をx軸に2移動させました・放物線の平行移動は2通りのやり方で処理する!1書き換え戦法!x 軸方向に 「 - 3 」平行移動するときは、 x を 「 x 3 」 に書き換える!べようとする。 2次関数のグラフの 2次関数のグラフの グラフの平行移動に b2 c2 d2 a2 2次関数の表、式、 特徴を考察することが 位置関係、グラフと式 ついて理解している。 グラフの相違点に関心 できる。 との関係を把握し、グ
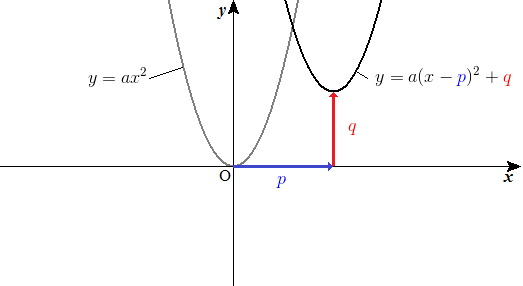
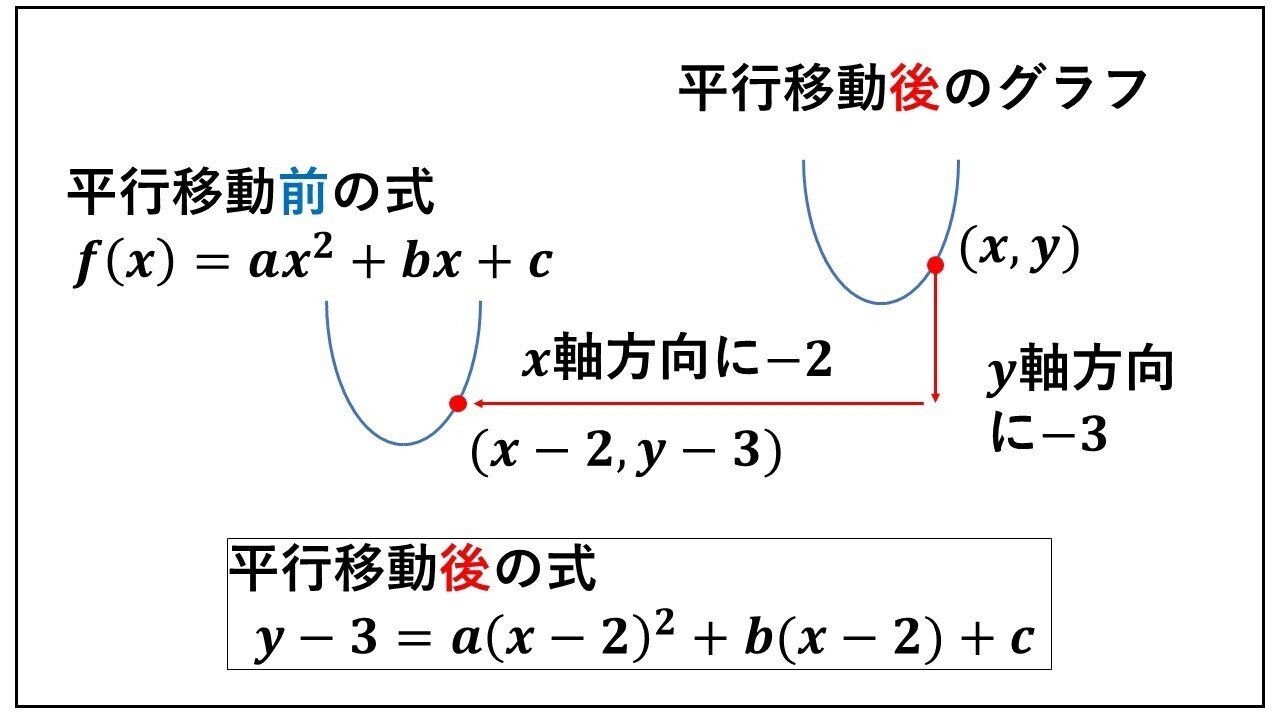
平行移動された式は\(x^2\)の係数である\(a\)の値が等しい。 という点です。 つまり、今回の問題では 『グラフが放物線\(y=3x^22x1\)を平行移動したもので』 という部分から 『新たに作りたい二次関数の式の\(a\)は-3になる』 ということが読み取れます。 二次関数の平行移動 y = a x 2 y=ax^2 y = a x 2 を平行移動させたグラフで頂点が (p, q) (p,q) (p, q) となるものは, y − q = a (x − p) 2 yq=a(xp)^2 y − q = a (x − p) 2 となります。 x x x 軸方向に p p p , y y y 軸方向に q q q 平行移動です。 円の平行移動 中心 (a, b) (a,b) (a, b) ,半径 r r r の円の方程式は,2 次 関数 平行 移動 2 次 関数 平行 移動。 質問数学(2次関数):平行移動で符号が逆? になることについて この計算方法の学習は、 次回からです。 で、これを y=x 2+3x-3 に入れていくわけですが、この式の x, y というのは「移動前の x, y」の
2次関数の平行移動 《解説》 2つの2次関数のグラフは, x 2の係数 a が一致すれば同じ形で,平行移動によって重なります. 2次関数のグラフの平行移動 グラフの平行移動 とは、 グラフをx軸方向やy軸方向に沿って移動させる ことです。 グラフの平行移動では、直線の傾きが変わったり、曲線の曲がり具合が変わったりすることはないので注意しましょう。 学年 高校1年生, 教科書 数Ⅰ 数研出版, キーワード 2次関数,平行移動,対称移動,2次関数の決定,二次関数,2次関数




2次関数のグラフ
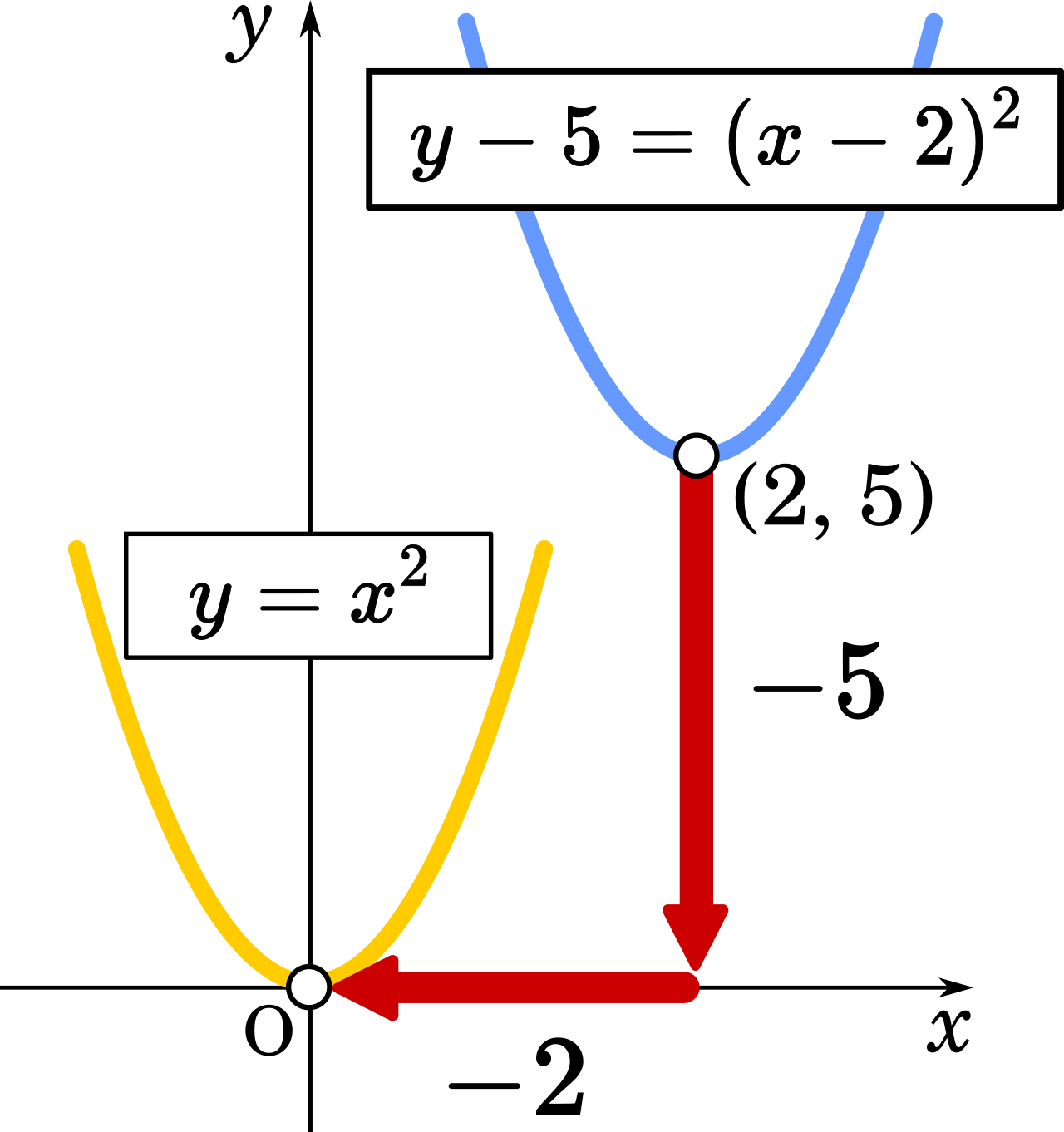



数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書
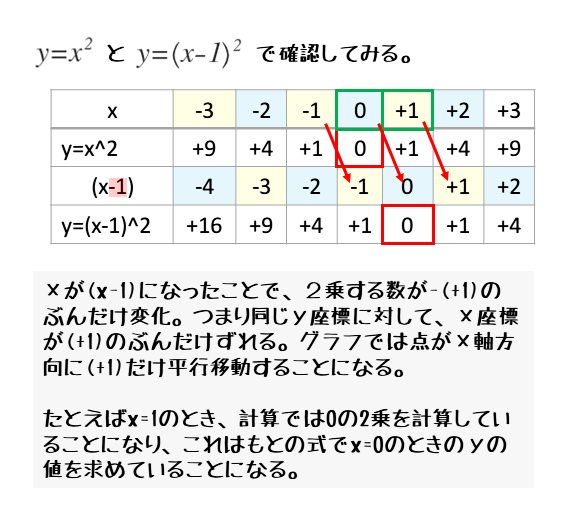
これの際たる例は 二次関数 です。二次関数では最初に \(\displaystyle y=x^{2}\) からスタートしてこれを平行移動することによって \(\displaystyle y=(xp)^{2}q\) が書けるので、 すべての二次関数をこの形にできればグラフは書けるようになりました よね。 高校数学:2次関数の平行移動②グラフの平行移動 こんにちは。相城です。今回は2次関数を実際に平行移動させていきましょう。仕組み的には頂点を移動させれば, グラフは平行移動しますのでそのあたりをみて, 最終的な解法にたどり着ければと思います。平行移動後のグラフの式はy=2x2です。y方向に2平行移動するので、yの値を2すればよいですね。 平行移動と二次関数の関係 二次関数の平行移動を考えます。一次関数と考え方は同じです。y=x 2 がx方向に3平行移動するとき、下図のようなグラフとなります。



進むのにマイナスとは これ如何に 図形の平行移動 理系男子の独り善がり




標準 二次曲線の平行移動 なかけんの数学ノート
今回の研究授業は,数学Ⅰ(2次関数の平行移動)についての授業を定時制通信制部会で協議・検討し, 行ったものである.関数に苦手意識をもつ定時制の生徒に対し,興味・関心を高める工夫として,ICT 機 器による視覚的効果を考えた.具体的には,PCを一人づつ操作させることも考えたが,生徒のPC操作習 得状況を考慮し,授業での提示方法となった.平行移動に対するイメージは印象付き,興味 2次関数の平行移動の解き方まとめ パターン①⋯ 頂点を求めてから移動させる(平方完成) 式を \( y=a(xp)^2q \) の形に直し、頂点の座標を求める。 平行移動させた後の頂点の座標を求める。 ②で求めた頂点で計算をする。 0403二次関数の平行、対称移動(難易度2) 19/3/18 19/3/21 問題 関数を y 軸に対称移動し、 x 軸に 2 、y軸に − 1 平行移動すると、 y = − x 2 2 x 3 の関数となった。 元の関数を求めよ ヒント 対称移動と平行移動したときの、変数の置き換えを使います



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん




2次関数21 12 平行移動対称移動のよくある誤謬 怜悧玲瓏 高校数学を天空から俯瞰する
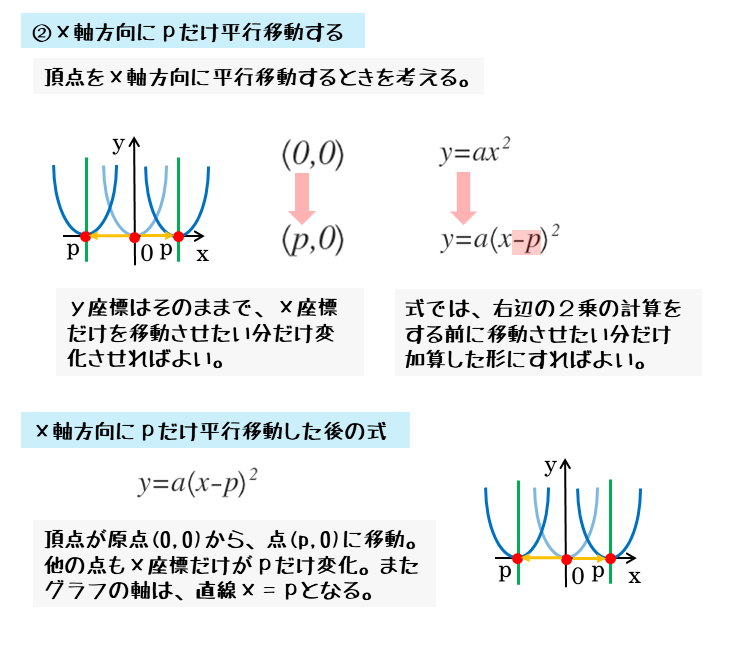
二次関数のグラフの平行移動 x x 軸方向に α α y y 軸方向に β β 平行移動 ・標準形 y=a(x−p)2q y = a ( x − p) 2 q を平行移動すると y=a(x−p−α)2 qβ y = a ( x − p − α) 2 q β ・一般形 y=ax2 bxc y = a x 2 b x c を平行移動すると y−β=a(x−α)2b(x−α)c y − β = a ( x − α) 2 b ( x − α) c② は、① を、x軸方向に -b/2a 、y軸方向に -b 2 /4a +c 平行移動させたものだと分かる。 → よって、2乗の係数さえ等しければ、2つの2次関数は形状が等しいことになる(平行移動させたものなので) 二次関数 $y=x^2$ のグラフを $x$ 軸方向に $p$ 、$y$ 軸方向に $q$ 平行移動するとき、式は以下のように表すことができる。 $y=(xp)^2q$ $y=(x2)^25$ の $5$ を左辺に移項すると、このような式になります。




数 2次関数 対称移動 1つの知識から広く深まる世界 教えたい 人のための 数学講座




平行移動した曲線の方程式 数学 そーまのブログ屋さん
2次関数の平行移動 問題 y=2x²を平行移動した放物線が点(1、ー2)を通る。また、この放物線の頂点がy=ー2x²上にあるとき、このグラフの式を求めなさい。 y=ax²のグラフを平行移動して、2次関数の平行移動の続き を勉強していきます。 放物線の平行移動は平方完成が基本。 早速ではありますが、今回も問題を見てみましょう。 なんか難しそうな雰囲気ですよね。 ちなみに、これ 看護受験で出題される可能性 がかなり高い問題です。 このページでは、 数学Ⅰの「2次関数の平行移動」について解説します 。 平行移動の公式と計算方法を,具体的に問題を解きながらわかりやすく解説していきます。公式の丸暗記だけでなく、「なぜ平行移動の公式がマイナスになるのか」理解することが重要です。




頂点の平行移動が公式だけすぐにわかる方法 看護受験の必須 数学の公式を確認テスト Vol23 Kazアカデミー 大阪の看護学校 看護予備校




2次関数のグラフを 原点 X K Y Lに関して移動する方法 数学i By はっちゃん マナペディア
Sway is an easytouse digital storytelling app for creating interactive reports, presentations, personal stories and more Its builtin design engine helps you create professional designs in minutes With Sway, your images, text, videos, and other multimedia all flow together in a way that enhances your story Sway makes sure your creations look great on any screen2次関数No2「平行移動」 今回は2次関数の第2回、平行移動を解説します。平行移動については、次のことを覚 えてください。 平行移動 曲線y = f(x) をx 軸方向にp,y 軸方向にq だけ平行移動した曲線の方程式は y q = f(x p)となる。 上記が「なぜ成立するか? 文字を使って説明してみる。 y = a (x − p) 2 q の形に変形する y = a (x − p) 2 q を x 軸方向に j 、 y 軸方向に k 平行移動した時




2次関数のグラフ一覧 数学教材の倉庫



1
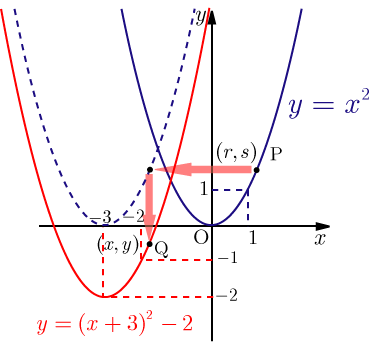
元の放物線の式を 「平方完成」 して、 頂点 を求めると、次のようになるよ。 元の放物線の頂点 (1,-1) を 「x軸方向に-1、y軸方向に4、平行移動」 しよう。 x座標 1-1=0 y座標 -1+4=3 つまり、求める放物線の頂点の座標は(0,3)だよ。 あとは、今日のポイント 「x 2 の係数は同じまま」 を使うことで、解答にたどり着けるよ。 答え 放物線を平行移動させるときは、すべての点がずれていく。例えばもとの放物線の1点を考えてみると(0,5)⇒(2,8)となる、 逆に、求める放物線のある1点(〇, )を、もとの放物線上の点に戻すと、(〇2, 3)になる ので、これをもとの放物線に代入すると 数学・算数 2次関数の平行移動 「2次関数y=-2x^2+x-2のグラフを平行移動したもので、次の条件を満たす放物線の方程式を求めよ。条件:x軸に接し、点(1、-8)を通る」という問題で、2次関数 質問no




二次関数の平行移動の問題です 答えは2枚目です 解説の解き方がいまいちわかりません Clear



1 C を定数とする 2 次関数 Y X2 のグラフを 2 点 C 0 C 4 0 を通るよう に平行移動して
テーラー展開のズレを感じよう。 楕円の軌跡(シミレーション) 平方根の利用 コピー用紙まず、2次関数に限らず、実際の平行移動の問題を解くに当たっては、x軸方向に+p、y軸方向に+q 平行移動させる場合、符号をひっくり返して、x を x-p、y を y-q で置き換えるという操作をしてもらったら結構です。




数学 2次関数 平行移動 基本 オンライン無料塾 ターンナップ



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん



48s96ub7b0z5f Net Nijikansu Taisyoido




高校数 2次関数 平行移動 オンライン無料塾 ターンナップ Youtube




2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係




二次関数 グラフの平行移動を具体例で詳細解説 式の仕組みから理解できます Rikeinvest
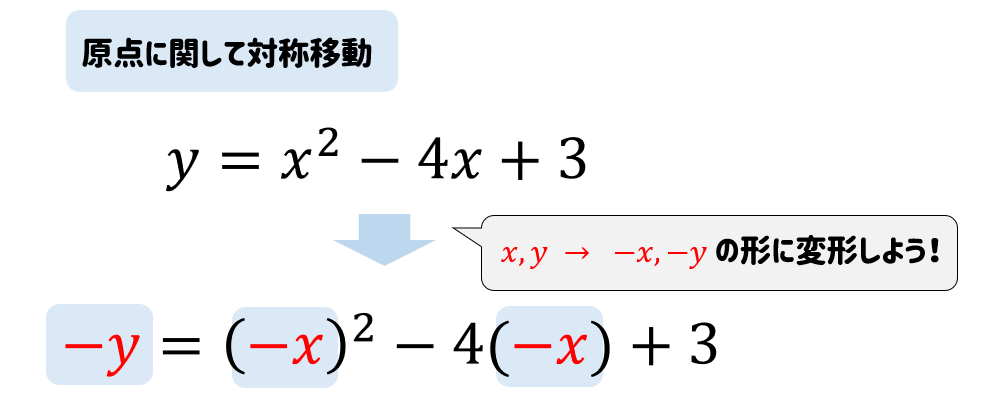



苦手な人向け 二次関数を対称移動したときの式の求め方を解説 数スタ



2 1leqxleq2 Descubre Como Resolverlo En Qanda



二次関数の移動




平行移動のやり方と公式の意味 符号を入れ替えて書き換えるだけで グラフの問題がスラスラ解ける 青春マスマティック




X 2 Y 1 Descubre Como Resolverlo En Qanda




二次関数 どのように平行移動したら重なる 例題を使って問題解説 数スタ




まなてぃ先生 鈴木真人 Twitterren 二次関数の平行移動と平方完成のまとめ スペースの関係で平行移動が結果論になってるのが悔やまれる リツイート歓迎です 数学 勉強 受験 ノート まとめ




2次関数の対称移動 数学i フリー教材開発コミュニティ Ftext



1




高校数学 放物線の平行移動1 重ねる 練習編 映像授業のtry It トライイット




放物線ヨコ平行移動が式と逆な感じがする話題をサマータイムと絡めて話してみた すうがくブログ 式変形ch




数 2次関数 関数の平行移動 操作は簡単 意味は深い 教えたい 人のための 数学講座



1




二次関数 平行移動したものが2点を通る式を作る方法とは 数スタ




3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ




3x22 1v41 3 141esquare 1 Descubre Como Resolverlo En Qanda
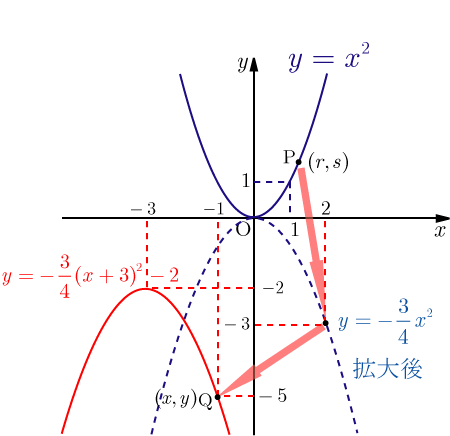



2次関数のグラフの拡大 平行移動に関する問題




2次関数の問題に対する条件反射 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
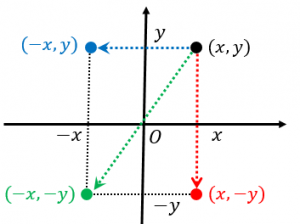



二次関数のx軸 Y軸 原点に関する対称移動 具体例で学ぶ数学



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス



平行移動するとなぜマイナスするの




数学 2次関数のグラフの平行移動のやり方とコツ 教科書より詳しい高校数学




数学i 2次関数 2 6 放物線の平行移動 1 Youtube




2次関数のグラフの平行移動 数学i By はっちゃん マナペディア




2次関数のグラフ グラフの平行移動 高校数学の無料オンライン学習サイトko Su




3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ




公式 関数の平行移動について解説するよ 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




高校数学 2次関数のグラフの対称移動の原理 X軸 Y軸 原点 受験の月




図解 グラフの平行移動がなぜマイナスで書かれるか本気で解説してみた 理系のひとりごと



Tikz 高校数学 2次関数の平行移動 数樂管理人のブログ
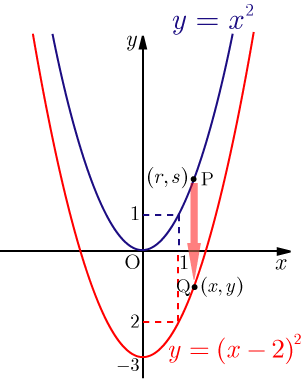



2次関数のグラフの平行移動に関する問題




2次関数の平行移動 数学i フリー教材開発コミュニティ Ftext




3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ



平行移動とは グラフ 二次関数など の平行移動の公式と作図 受験辞典



二つの2次関数グラフの位置関係 平行移動 2 Excel Vba デジタル教科書 電子教科書
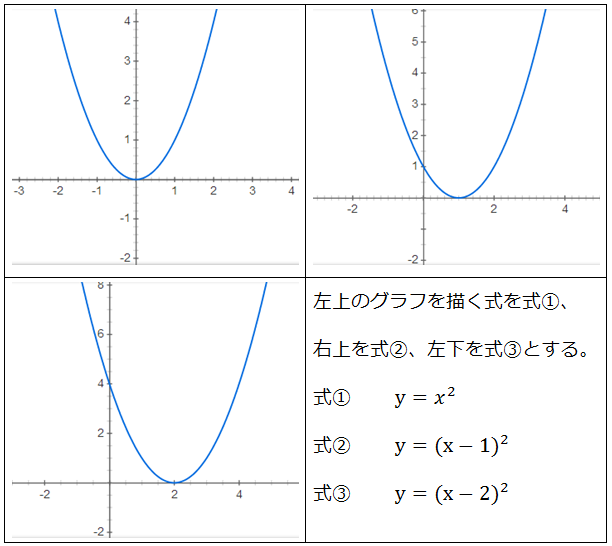



2次関数のグラフの平行移動 現代 Note



1 2 Yx24x5 X 3 Y Descubre Como Resolverlo En Qanda



平行移動とは 1分でわかる意味と定義 やり方 二次関数との関係



2次関数の平行移動 2 Geogebra




何回やっても答えにたどりつけません 何が違うのか教えてください Clear




2次関数のグラフの平行移動 落ちこぼれ数学科の学び直し数学




2次関数のグラフの対称移動 Y Ax Bx Cのグラフをx軸 Y軸 原点に関して対称移動 数学i By ふぇるまー マナペディア
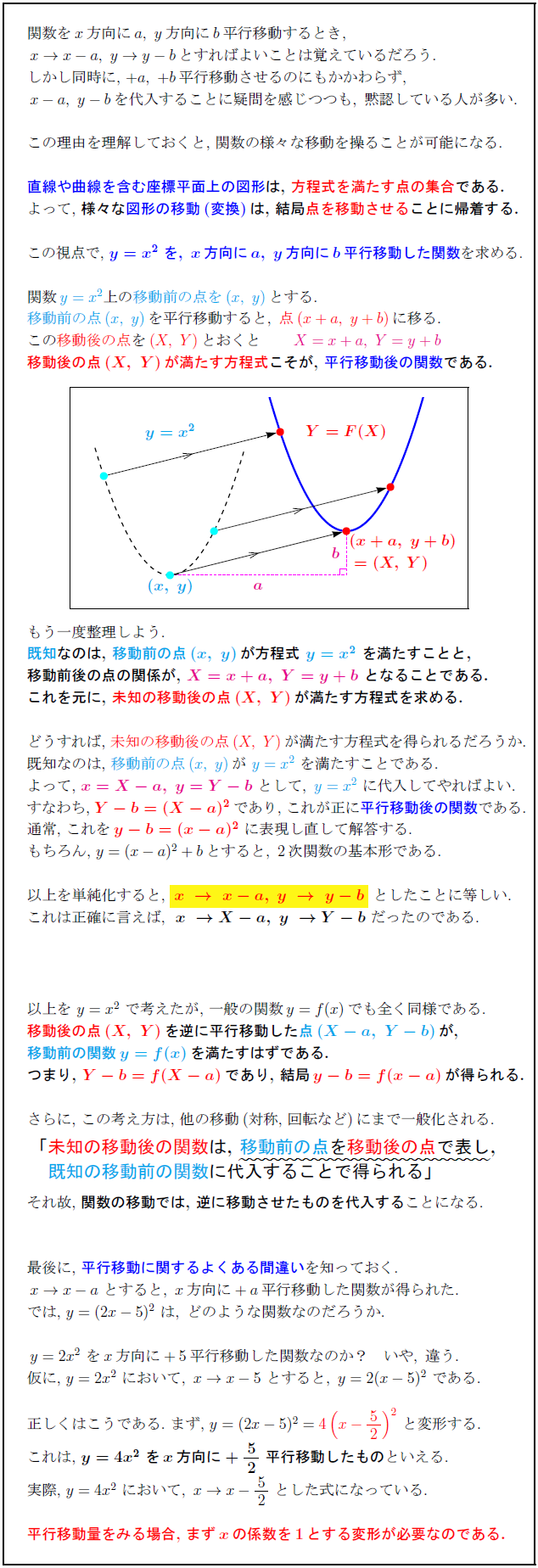



高校数学 平行移動の原理 X方向に A平行移動するのにx Aを代入する理由 受験の月
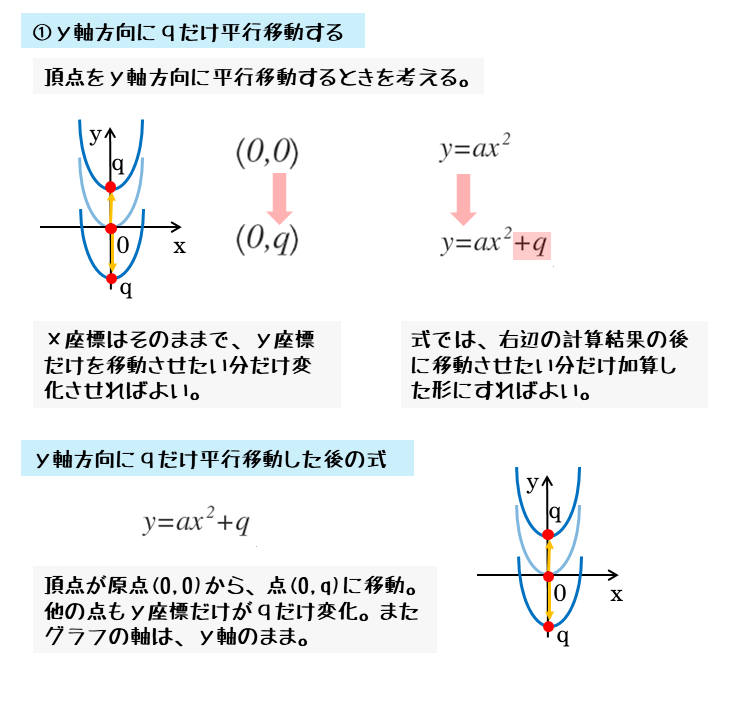



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん



まとめ 2 2 二次関数のグラフの平行移動 対称移動 わかりmath



二次関数の移動



2次関数のグラフの平行移動に関する問題



例題で学ぶ高校数学 平行移動した三角関数のグラフ



二次関数のグラフの平行移動 Geogebra



2次関数のグラフの平行移動 上に凸 Androidアプリ Applion




高校数学 Y A X P 2のグラフ2 練習編 映像授業のtry It トライイット




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
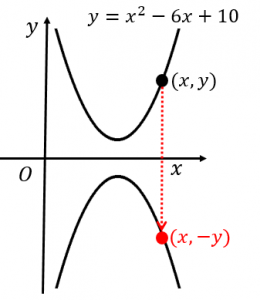



二次関数のx軸 Y軸 原点に関する対称移動 具体例で学ぶ数学



Ivoxx9sqqpxvqm




まなてぃ先生 鈴木真人 Twitterren 二次関数の平行移動と平方完成のまとめ スペースの関係で平行移動が結果論になってるのが悔やまれる リツイート歓迎です 数学 勉強 受験 ノート まとめ




2次関数の移動に関する問題まとめ チャート 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




二次関数のグラフの平行移動とは 公式や応用問題3選をわかりやすく解説 遊ぶ数学



数1の問題です 二次関数の平行移動の問題で 答えの数字自体はあっているのに Yahoo 知恵袋




数 2次関数 関数の決定その1 頂点と軸が分かる場合 平行移動と媒介変数がポイント 教えたい 人のための 数学講座




高校数学 二次関数の平行移動 対称移動 Youtube




高校数学 2次関数の平行移動 Youtube




高校数学 数 41 2次関数 移動編 Youtube



1
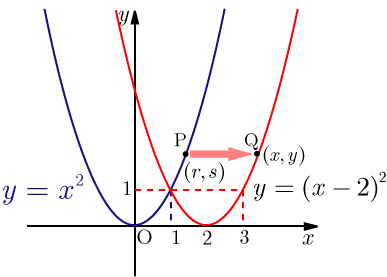



2次関数のグラフの平行移動に関する問題




2次関数3 平行移動の指導はどうしようか 怜悧玲瓏 高校数学を天空から俯瞰する




2次関数 放物線の平行移動 高校数学 放物線を重ねてみようの巻 Vol 13 Kazアカデミー 大阪の看護学校 看護予備校




高校数学 2次関数のグラフの平行移動の原理 受験の月




2 関数のグラフの移動 ノート ひまわり数学教室



48s96ub7b0z5f Net Nijikansu Heikoido




高校数学 数 勉強動画 2次関数 移動編の問題 19ch




必読 関数のグラフに関する指導の要点まとめ 基本の き 塾講師ステーション情報局




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



グラフの平行移動 高校数学の無料オンライン学習サイトko Su
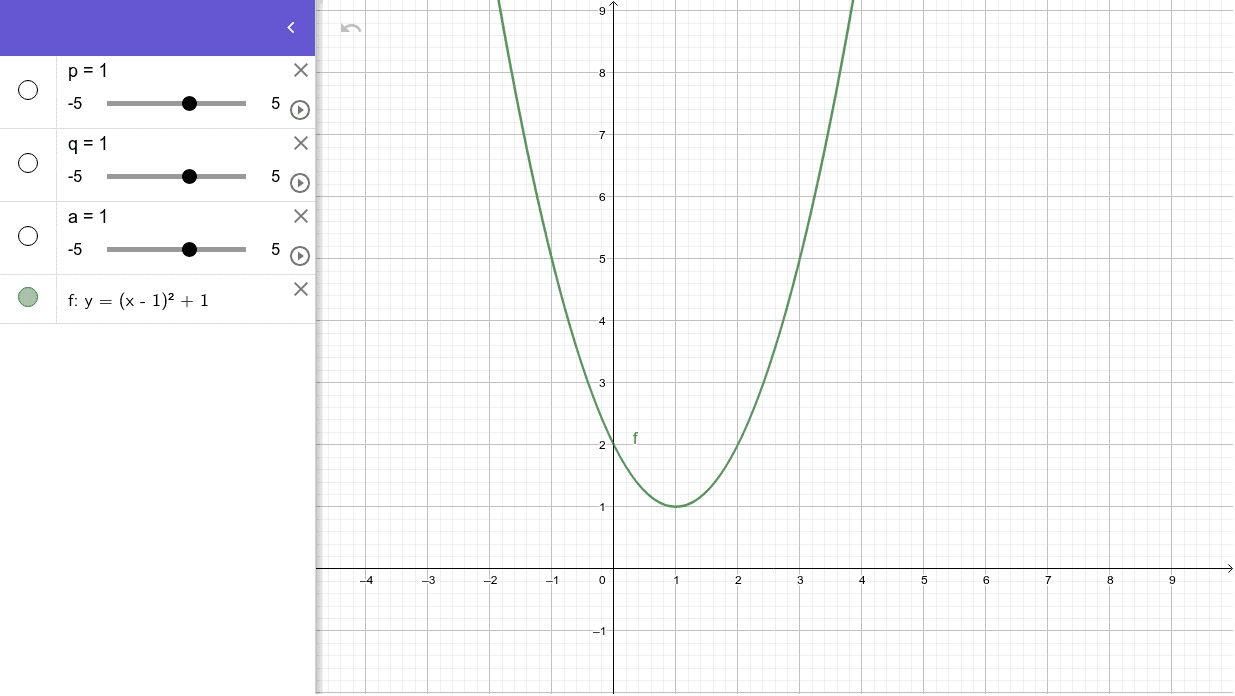



二次関数の平行移動 Geogebra




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
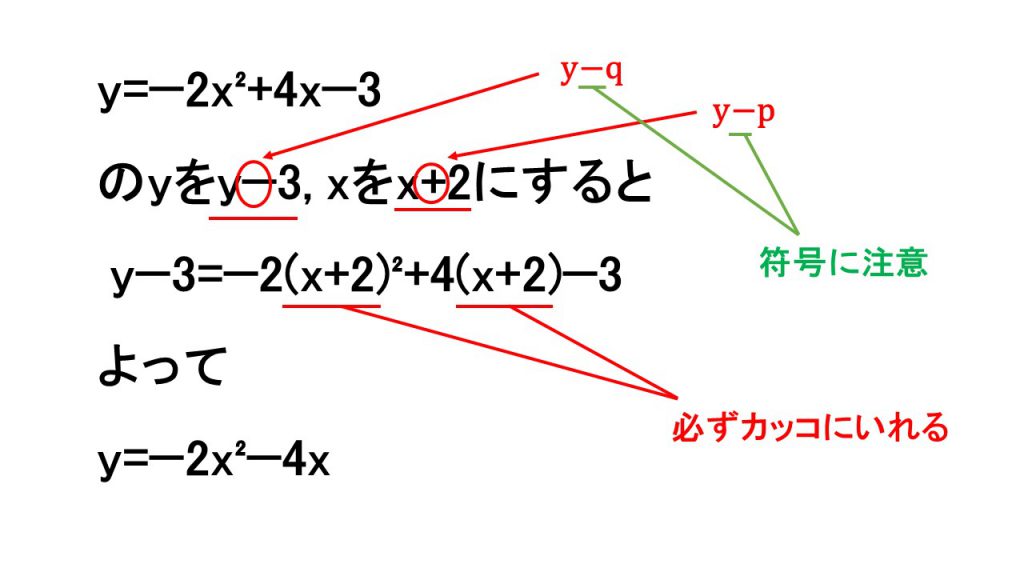



二次関数の平行移動 大学受験の王道




至急お願いします 放物線の平行移動です Clear



高1の二次関数の平行移動の時 ある放物線をx軸方向に1 y Yahoo 知恵袋
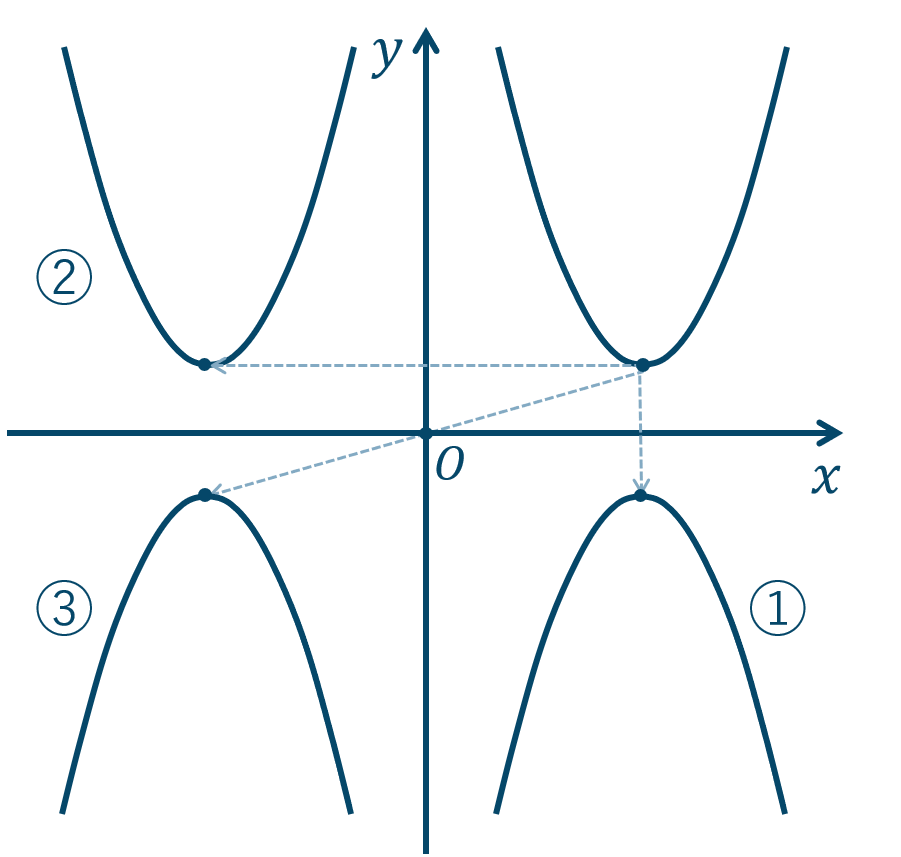



数学 グラフの対称移動のやり方とコツ ページ 2 教科書より詳しい高校数学



平行移動とは 1分でわかる意味と定義 やり方 二次関数との関係




二次関数の平行移動 大学受験の王道
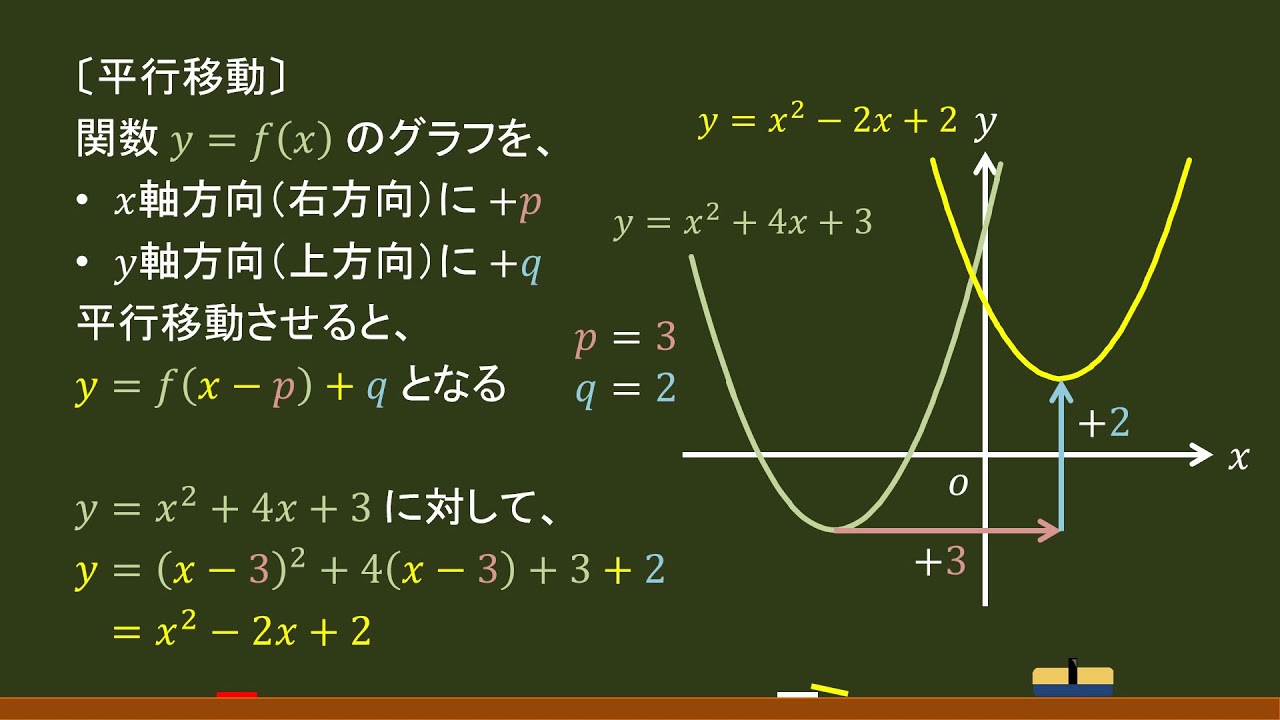



高校数 2次関数 平行移動 オンライン無料塾 ターンナップ Youtube




二次関数とグラフ 中3数学 高校数学 Irohabook


コメント
コメントを投稿